POLÍTICA DE PRIVACIDADE
Este site é mantido e operado por Luis Carlos Cyrino Peres
Nós coletamos e utilizamos alguns dados pessoais que pertencem àqueles que utilizam nosso site. Ao fazê-lo, agimos na qualidade de controlador desses dados e estamos sujeitos às disposições da Lei Federal n. 13.709/2018 (Lei Geral de Proteção de Dados Pessoais - LGPD).
Nós cuidamos da proteção de seus dados pessoais e, por isso, disponibilizamos esta política de privacidade, que contém informações importantes sobre:
- Quem deve utilizar nosso site
- Quais dados coletamos e o que fazemos com eles;
- Seus direitos em relação aos seus dados pessoais; e
- Como entrar em contato conosco.
1. Dados que coletamos e motivos da coleta
Nosso site coleta e utiliza alguns dados pessoais de nossos usuários, de acordo com o disposto nesta seção.
1.1. Dados pessoais fornecidos expressamente pelo usuário
Nós coletamos os seguintes dados pessoais que nossos usuários nos fornecem expressamente ao utilizar nosso site:
Nome
E-mail
Telefone
A coleta destes dados ocorre nos seguintes momentos:
Solicitação de Contato
Solicitação de Orçamentos
Os dados fornecidos por nossos usuários são coletados com as seguintes finalidades:
Para retornar o contato ao usuário que solicitou, seja para orçamento, duvidas ou suporte
1.2. Dados pessoais obtidos de outras formas
Nós coletamos os seguintes dados pessoais de nossos usuários:
Dados de localização, navegador, dispositivo de acesso, sistema operacional, faixa etária, sexo, através do Google Analytics e Google Ads
A coleta destes dados ocorre nos seguintes momentos:
Ao acessar o site e navegar nas páginas
Estes dados são coletados com as seguintes finalidades:
Melhorar a experiência do usuário ao navegar em nosso site
1.3. Dados sensíveis
Não serão coletados dados sensíveis de nossos usuários, assim entendidos aqueles definidos nos arts. 11 e seguintes da Lei de Proteção de Dados Pessoais. Assim, não haverá coleta de dados sobre origem racial ou étnica, convicção religiosa, opinião política, filiação a sindicato ou a organização de caráter religioso, filosófico ou político, dado referente à saúde ou à vida sexual, dado genético ou biométrico, quando vinculado a uma pessoa natural.
1.4. Cookies
Cookies são pequenos arquivos de texto baixados automaticamente em seu dispositivo quando você acessa e navega por um site. Eles servem, basicamente, para seja possível identificar dispositivos, atividades e preferências de usuários.
Os cookies não permitem que qualquer arquivo ou informação sejam extraídos do disco rígido do usuário, não sendo possível, ainda, que, por meio deles, se tenha acesso a informações pessoais que não tenham partido do usuário ou da forma como utiliza os recursos do site.
a. Cookies de terceiros
Alguns de nossos parceiros podem configurar cookies nos dispositivos dos usuários que acessam nosso site.
Estes cookies, em geral, visam possibilitar que nossos parceiros possam oferecer seu conteúdo e seus serviços ao usuário que acessa nosso site de forma personalizada, por meio da obtenção de dados de navegação extraídos a partir de sua interação com o site.
O usuário poderá obter mais informações sobre os cookies de terceiro e sobre a forma como os dados obtidos a partir dele são tratados, além de ter acesso à descrição dos cookies utilizados e de suas características, acessando o seguinte link:
https://developers.google.com/analytics/devguides/collection/analyticsjs/cookie-usage?hl=pt-br
As entidades encarregadas da coleta dos cookies poderão ceder as informações obtidas a terceiros.
b. Gestão de cookies
O usuário poderá se opor ao registro de cookies pelo site, bastando que desative esta opção no seu próprio navegador. Mais informações sobre como fazer isso em alguns dos principais navegadores utilizados hoje podem ser acessadas a partir dos seguintes links:
Internet Explorer:
https://support.microsoft.com/pt-br/help/17442/windows-internet-explorer-delete-manage-cookies
Safari:
https://support.apple.com/pt-br/guide/safari/sfri11471/mac
Google Chrome:
https://support.google.com/chrome/answer/95647?hl=pt-BR&hlrm=pt
Mozila Firefox:
https://support.mozilla.org/pt-BR/kb/ative-e-desative-os-cookies-que-os-sites-usam
Opera:
https://www.opera.com/help/tutorials/security/privacy/
A desativação dos cookies, no entanto, pode afetar a disponibilidade de algumas ferramentas e funcionalidades do site, comprometendo seu correto e esperado funcionamento. Outra consequência possível é remoção das preferências do usuário que eventualmente tiverem sido salvas, prejudicando sua experiência.
1.5. Coleta de dados não previstos expressamente
Eventualmente, outros tipos de dados não previstos expressamente nesta Política de Privacidade poderão ser coletados, desde que sejam fornecidos com o consentimento do usuário, ou, ainda, que a coleta seja permitida com fundamento em outra base legal prevista em lei.
Em qualquer caso, a coleta de dados e as atividades de tratamento dela decorrentes serão informadas aos usuários do site.
2. Compartilhamento de dados pessoais com terceiros
Nós não compartilhamos seus dados pessoais com terceiros. Apesar disso, é possível que o façamos para cumprir alguma determinação legal ou regulatória, ou, ainda, para cumprir alguma ordem expedida por autoridade pública.
3. Por quanto tempo seus dados pessoais serão armazenados
Os dados pessoais coletados pelo site são armazenados e utilizados por período de tempo que corresponda ao necessário para atingir as finalidades elencadas neste documento e que considere os direitos de seus titulares, os direitos do controlador do site e as disposições legais ou regulatórias aplicáveis.
Uma vez expirados os períodos de armazenamento dos dados pessoais, eles são removidos de nossas bases de dados ou anonimizados, salvo nos casos em que houver a possibilidade ou a necessidade de armazenamento em virtude de disposição legal ou regulatória.
4. Bases legais para o tratamento de dados pessoais
Uma base legal para o tratamento de dados pessoais nada mais é que um fundamento jurídico, previsto em lei, que justifica o justifica. Assim, cada operação de tratamento de dados pessoais precisa ter uma base legal a ela correspondente.
Nós tratamos os dados pessoais de nossos usuários nas seguintes hipóteses:
- mediante o consentimento do titular dos dados pessoais
- para o cumprimento de obrigação legal ou regulatória pelo controlador
4.1. Consentimento
Determinadas operações de tratamento de dados pessoais realizadas em nosso site dependerão da prévia concordância do usuário, que deverá manifestá-la de forma livre, informada e inequívoca.
O usuário poderá revogar seu consentimento a qualquer momento, sendo que, não havendo hipótese legal que permita ou que demande o armazenamento dos dados, os dados fornecidos mediante consentimento serão excluídos.
Além disso, se desejar, o usuário poderá não concordar com alguma operação de tratamento de dados pessoais baseada no consentimento. Nestes casos, porém, é possível que não possa utilizar alguma funcionalidade do site que dependa daquela operação. As consequências da falta de consentimento para uma atividade específica são informadas previamente ao tratamento.
4.2. Cumprimento de obrigação legal ou regulatória pelo controlador
Algumas operações de tratamento de dados pessoais, sobretudo o armazenamento de dados, serão realizadas para que possamos cumprir obrigações previstas em lei ou em outras disposições normativas aplicáveis às nossas atividades.
5. Direitos do usuário
O usuário do site possui os seguintes direitos, conferidos pela Lei de Proteção de Dados Pessoais:
- confirmação da existência de tratamento;
- acesso aos dados;
- correção de dados incompletos, inexatos ou desatualizados;
- anonimização, bloqueio ou eliminação de dados desnecessários, excessivos ou tratados em desconformidade com o disposto na lei;
- portabilidade dos dados a outro fornecedor de serviço ou produto, mediante requisição expressa, de acordo com a regulamentação da autoridade nacional, observados os segredos comercial e industrial;
- eliminação dos dados pessoais tratados com o consentimento do titular, exceto nos casos previstos em lei;
- informação das entidades públicas e privadas com as quais o controlador realizou uso compartilhado de dados;
- informação sobre a possibilidade de não fornecer consentimento e sobre as consequências da negativa;
- revogação do consentimento.
É importante destacar que, nos termos da LGPD, não existe um direito de eliminação de dados tratados com fundamento em bases legais distintas do consentimento, a menos que os dados seja desnecessários, excessivos ou tratados em desconformidade com o previsto na lei.
5.1. Como o titular pode exercer seus direitos
Para garantir que o usuário que pretende exercer seus direitos é, de fato, o titular dos dados pessoais objeto da requisição, poderemos solicitar documentos ou outras informações que possam auxiliar em sua correta identificaçãoo, a fim de resguardar nossos direitos e os direitos de terceiros. Isto somente será feito, porém, se for absolutamente necessário, e o requerente receberá todas as informações relacionadas.
6. Medidas de segurança no tratamento de dados pessoais
Empregamos medidas técnicas e organizativas aptas a proteger os dados pessoais de acessos não autorizados e de situações de destruição, perda, extravio ou alteração desses dados.
As medidas que utilizamos levam em consideração a natureza dos dados, o contexto e a finalidade do tratamento, os riscos que uma eventual violação geraria para os direitos e liberdades do usuário, e os padrões atualmente empregados no mercado por empresas semelhantes à nossa.
Entre as medidas de segurança adotadas por nós, destacamos as seguintes:
Armazenamento em servidores e computadores criptografados
Ainda que adote tudo o que está ao seu alcance para evitar incidentes de segurança, é possível que ocorra algum problema motivado exclusivamente por um terceiro - como em caso de ataques de hackers ou crackers ou, ainda, em caso de culpa exclusiva do usuário, que ocorre, por exemplo, quando ele mesmo transfere seus dados a terceiro. Assim, embora sejamos, em geral, responsáveis pelos dados pessoais que tratamos, nos eximimos de responsabilidade caso ocorra uma situação excepcional como essas, sobre as quais não temos nenhum tipo de controle.
De qualquer forma, caso ocorra qualquer tipo de incidente de segurança que possa gerar risco ou dano relevante para qualquer de nossos usuários, comunicaremos os afetados e a Autoridade Nacional de Proteção de Dados acerca do ocorrido, em conformidade com o disposto na Lei Geral de Proteção de Dados.
7. Reclamação a uma autoridade de controle
Sem prejuízo de qualquer outra via de recurso administrativo ou judicial, os titulares de dados pessoais que se sentirem, de qualquer forma, lesados, podem apresentar reclamação à Autoridade Nacional de Proteção de Dados.
8. Alterações nesta política
A presente versão desta Política de Privacidade foi atualizada pela última vez em: 02/12/2020.
Nos reservamos o direito de modificar, a qualquer momento, as presentes normas, especialmente para adaptá-las às eventuais alterações feitas em nosso site, seja pela disponibilização de novas funcionalidades, seja pela supressão ou modificação daquelas já existentes.
Sempre que houver uma modifição, nossos usuários serão notificados acerca da mudança.
9. Como entrar em contato conosco
Para esclarecer quaisquer dúvidas sobre esta Política de Privacidade ou sobre os dados pessoais que tratamos, entre em contato com nosso Encarregado de Proteção de Dados Pessoais, por algum dos canais mencionados abaixo:
E-mail: contato@manutencaoemfoco.com.br
Telefone: (41) 9 9958-6044

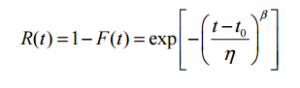
![]()
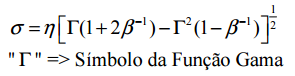





Caros Senhores,
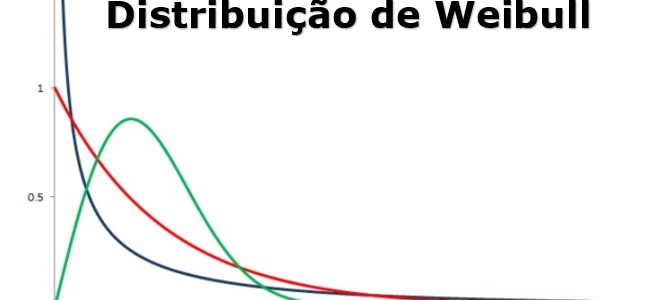
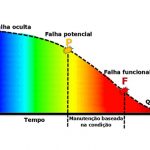
Gostaria de saber se vcs tem um exemplo de utilização da distribuição de Weibull. Pode ser simples mesmo. E como foi feita a coleta dos dados confiável.
Muito Obrigado. Fábio.